Peta Karnaugh

Belajar Peta Karnaugh

Peta Karnaugh

Peta karnaugh digunakan untuk mempermudah penyerdehanaan fungsi boolean baik untuk suku minterm atau maxterm.

Contoh peta karnaugh 3 variabel (A,B,C)

  

Deretan nomor di atas kotak bukan diurutan berdasarkan angka biner, namun berdasarkan deretan Gray Code dari metode dibawah.

Perlu juga diingat mengenai Rumus aljabar Boolean :

Or (“+”)	And (“.”)
a+(b+c)=(a+b)+c a+b=b+a a+(a.b)=a a+(b.c)=(a+b)(a+c) a+a’=1	a(b.c)=(a.b).c a.b=b.a a.(a+b)=a a.(b+c)=(a.b)+(a.c) a.a’=0

 -- Penulisan Peta karnauogh --

-- Misal : m₇+m₃ --

 m_{7 = 111}
 m_{3 = 011}

-- Peta Karnaugh 4x4 --

                                       

1.  Peta Karnaugh Suku Minterm (SOP – Sum of Product)

Misal didapat persamaan :

a.)    F = m₀ + m₁

Maka pemetaannya

F      = m₀ + m₁

     = A’B’C’ + A’B’C

   = (A’+A’)(B’+B’)(C’+C)

   = A’.B’.1

   = A’B’

b.)    F = A’B’C’ + A’B’C +A’BC +A’BC’

F   = A’B’C’ + A’B’C +A’BC +A’BC’

     = (A’+A’+A’+A’).(B’+B’+B+B).
        (C’+C+C+C’)

     = A’.1.1

     = A’

c.)     F = A’B’C + A’BC + AB’C + ABC         

F  = A’B’C + A’BC + AB’C + ABC

     = C

d.)    F = A’B’C’ + AB’C’ + A’BC’ + ABC’

F = A’B’C’ + AB’C’ + A’BC’ + ABC’

     = C’

Contoh Soal Minterm :
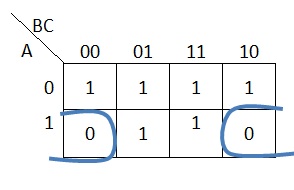
 1. Sederhanakan F = A’B’C’ + A’B’C + A’BC + A’BC’ + A’B’C + A’BC + AB’C + ABC

F =   A’B’C’ + A’B’C + A’BC + A’BC’ + A’B’C
        + A’BC + AB’C + ABC

   = (A’B’C’ + A’B’C + A’BC + A’BC’)
      + (A’B’C + A’BC + AB’C + ABC)

   = (A’) + (C)

   = A’ + C

2.       Sederhanakan diagram logika berikut

Jawab :

Output =       I    +   II     +  III

                               = A’B’C + AB’C + AB’C’

Output   = A’B’C + AB’C + AB’C’
              = (A’B’C + AB’C) + (AB’C’
                   + AB’C)

              = B’C + AB’

Sehingga dapat disederhanakan menjadi :

 

                                                                    

2.  Peta Karnaugh Suku Maxterm (POS - Product of Sum)

Seperti halnya pada minterm pada maxterm metodenya hampir sama namun nilai 1 dianggap sebagai invers dari input sedangkan input menggunakan nilai 0.

Misal didapat persamaan :

a.) F = M₆ . M₇

Maka pemetaannya

 F = M₆ . M₇

     = (A’+B’+C) . (A’+B’+C’)

    = (A’.A’)+(B’.B’)+(C.C’)

    = A’+ B’+ 0

    = A’+B’

b.) F = (A’+B+C) . (A’+B+C’) . (A’+B’+C’) . (A’+B’+C)

F = (A’+B+C) . (A’+B+C’).
      (A’+B’+C’) . (A’+B’+C)

   = A’

c.) F = (A+B+C) (A+B’+C) (A’+B+C) (A’+B’+C)      

F  = (A+B+C) (A+B’+C)
       (A’+B+C) (A’+B’+C)

     = C

d.) F = (A+B+C’)  (A+B’+C’) (A’+B+C’) (A’+B’+C’)

F = (A+B+C’) (A+B’+C’)
      (A’+B+C’) (A’+B’+C’)

   = C’

Soal Maxterm :

1. Sederhanakan F = (A’+B+C).(A’+B”C)

F = (A’+B+C).(A’+B’+C)

   = A’+ C

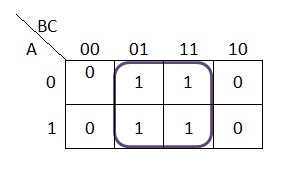
2. Sederhanakan peta karnaough dibawah dan buat diagram output penyederhanaannya!

F = [ (A+B+C)(A+B’+C) ] . [ (A+B’+C’)
         (A+B’+C)(A’+B’+C’)(A’+B’+C) ]

   = [A+C].[B’]

   = (A+C).B’

Kesimpulan :

Dari contoh minterm dan maxterm terdapat beberapa kesamaan jika ditinjau menurut peta dan hasil penyederhanaan. Hal ini dapat dilihat pada:

1. Contoh 1 minterm

           F = A’ + C

Contoh 1 Maxterm

F = (A’+B+C).(A’+B’+C)

   = A’+ C

Dari bentuk peta karnaugh yang sama namun perhitungan berbeda (minterm dan maxterm) memiliki hasil F yang sama diantara keduanya.

Sehingga pada dasarnya suatu peta karnaugh dapat diselesaikan menggunakan dua metode yaitu maxterm atau minterm sesuai kebutuhan.

2. Pada contoh soal 2 tidak jauh beda

Jika ditinjau dari persamaan boolean maka keduanya memiliki nilai yang sama :

B’.(A+C) = B’C + B’A

Namun jika dilihat dari segi efisiensi komponen maka maxterm lebih efisien (1 “OR” dan 1 “And”) dibanding minterm ( 2 “And” dan 1 “OR”). Namun bukan berarti minterm lebih boros dari maxterm hal ini tergantung dari hasil akhir perhitungan kedua metode.